An Introduction to Statistical Machine Learning
More than seventy years have passed since the renowned American mathematician Samuel S. Wilks famously stated, "Statistical thinking will one day be as necessary for efficient citizenship as the ability to read and write," paraphrasing HG Wells' book, Mankind in the Making. While this statement may have been somewhat exaggerated, its underlying message about the significance of statistics remains relevant in today's information age.

(Image Source: The American Statistical Association)
With the rapid progress of technology and unprecedented innovation, machine learning and Generative AI have taken center stage. These advancements have profoundly influenced our personal lives and facilitated data-driven decision-making on a larger scale.
However, amidst all the buzz surrounding these cutting-edge technologies, statistics continue to play a crucial role. Statistical inference remains the bedrock of numerous technological breakthroughs, particularly within the realm of machine learning. It is inseparable from the very essence of data, which is the foundation for all the exciting new technologies surrounding us.
Let’s unmask the magic of statistical machine learning together!
What is Statistical Machine Learning?
As intuitive as it sounds from its name, statistical machine learning involves using statistical techniques to develop models that can learn from data and make predictions or decisions.
You might have heard technical terms such as supervised, unsupervised, and semi-supervised learning– they all rely on a solid statistical foundation.
In essence, statistical machine learning merges the computational efficiency and adaptability of machine learning algorithms with statistical inference and modeling capabilities.
By employing statistical methods, we can extract significant patterns, relationships, and insights from intricate datasets, thereby promoting the effectiveness of machine learning algorithms.
The Role of Statistics in Machine Learning
Statistics constitutes the backbone of machine learning, providing the tools and techniques to analyze and interpret data.
Essentially, statistics provides the theoretical framework upon which machine learning algorithms are built.
Statistics is the science that allows us to collect, analyze, interpret, present, and organize data. It provides a robust set of tools for understanding patterns and trends, and making inferences and predictions based on data. When we're dealing with large datasets, statistics helps us understand and summarize the data, allowing us to make sense of complex phenomena.
Machine learning, on the other hand, is a powerful tool that allows computers to learn from and make decisions or predictions based on data. The ultimate goal of machine learning is to create models that can adapt and improve over time, as well as generalize from specific examples to broader cases.
This is where the beauty of the fusion between statistics and machine learning comes to light. The principles of statistics are the very pillars that uphold the structure of machine learning.
- Constructing machine learning models. Statistics provides the methodologies and principles for creating models in machine learning. For instance, the linear regression model leverages the statistical method of least squares to estimate the coefficients.
- Interpreting results. Statistical concepts allow us to interpret the results generated by machine learning models. Measures such as p-value, confidence intervals, R-squared, and others provide us with a statistical perspective on the machine learning model’s performance.
- Validating models. Statistical techniques are essential for validating and refining the machine learning models. For instance, techniques like hypothesis testing, cross-validation, and bootstrapping help us quantify the performance of models and avoid problems like overfitting.
- Underpinning advanced techniques. Even some of the more complex machine learning algorithms, such as Neural Networks, have statistical principles at their core. The optimization techniques, like gradient descent, used to train these models are based on statistical theory.
As a result, a solid understanding of statistics not only allows us to better construct and validate machine learning models, but also enables us to interpret their outputs in a meaningful and useful way.
Let’s take a look at some of the key statistical concepts that are tightly related to machine learning. You can learn more about these concepts in our Statistics Fundamentals with Python skill track.
Probability
Probability theory is of utmost importance in machine learning as it provides the foundation for modeling uncertainty and making probabilistic predictions. How could we quantify the likelihood of different outcomes, events, or simply numerical values? Probability helps with that! In addition, Probability distributions are especially important in machine learning and make all the magic happen.
Some commonly used distributions include Gaussian (Normal), Bernoulli, Poisson, and Exponential distributions. We have a handy probability cheat sheet to act as a quick reference for probability rules.
Descriptive Statistics
Descriptive statistics enable us to understand the characteristics and properties of datasets. They help us summarize and visualize data, identify patterns, detect outliers, and gain initial insights that inform subsequent modeling and analysis.

Our descriptive statistics cheat sheet can help you learn these concepts
Measure of Central Tendency
The mean, median, and mode provide valuable insights into the central or representative values of a dataset. In machine learning, they aid in data preprocessing by assisting with the imputation of missing values and identifying potential outliers.
During feature engineering, they also come in handy in capturing the typical or most frequent values that impact model performance.
Variance and Standard Deviation
Variance and standard deviation quantify the spread or dispersion of data points around the central tendency. They serve as indicators of data consistency and variability in machine learning.
These measures are useful for feature selection or dimensionality reduction, identifying features with limited predictive power.
Additionally, they aid in assessing model performance by analyzing the variability of predictions or residuals, facilitating the evaluation and comparison of different algorithms.
Measure of Spread
Range, interquartile range, and percentiles are measures of spread that offer insights into the distribution of data values. They are particularly valuable in outlier detection, as they help identify and address outliers that can greatly influence model training and predictions. In cases where data needs to be transformed or normalized for better algorithm performance, these measures can provide guidance.
Sampling
Machine learning models are trained based on sampled data. If the samples are not carefully selected, the reliability of our models becomes uncertain. Ideally, we aim to choose representative subsets of data from larger populations.
Employing proper sampling techniques also ensures that machine learning models are trained on diverse and unbiased data, promoting ethical and responsible use of technology.
Check out our Sampling in Python course to learn more about this powerful skill.
Estimation
Estimation techniques are crucial in machine learning for determining unknown population parameters based on sample data. They allow us to estimate model parameters, evaluate model performance, and make predictions about unseen data.
The most common estimation method used in machine learning is Maximum Likelihood (ML) estimation, which finds the estimator of an unknown parameter by maximizing the likelihood function.
Hypothesis Testing
Hypothesis testing provides a systematic approach to evaluating the significance of relationships or differences in machine learning tasks. It enables us to assess the validity of assumptions, compare models, and make statistically significant decisions based on the available evidence.
Cross-Validation
Cross-Validation (CV) is a statistical technique used in machine learning to assess the performance and generalization error of an algorithm. Its primary purpose is to prevent overfitting, a phenomenon where the model performs well on the training data but fails to generalize to unseen data.
By dividing the dataset into multiple subsets and iteratively training and evaluating the model on different combinations, CV provides a more reliable estimate of the algorithm's performance on unseen data.
Popular Statistical Machine Learning Techniques
These complex statistical concepts are the first steps toward effective machine learning algorithms. Let’s now explore some of the most popular machine learning models and see how statistics helped achieve their remarkable capabilities.
Linear Regression
Linear regression is a term commonly encountered in the statistical literature, but it is more than just that. It is also seen as a supervised learning algorithm that captures the connection between a dependent variable and independent variables.
Statistics assist in estimating coefficients, conducting hypothesis tests, and evaluating the significance of the relationships, providing valuable insights and a deeper understanding of the data.
Explore the topic in more depth with our essentials of linear regression in Python tutorial or on our Introduction to Regression in R course.
Logistic Regression
Just like linear regression, logistic regression is a statistical classification algorithm that estimates the probability of categorical outcomes based on independent variables. By applying a logistic function, it predicts the occurrence of a particular class.
We have a full explanation of the topic in our understanding logistic regression in Python tutorial.
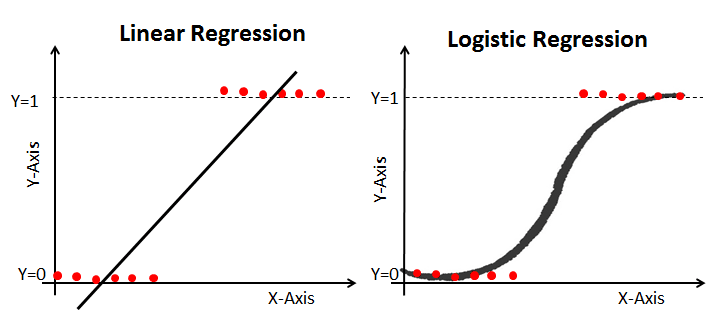
Logistic and linear regression
Decision Trees
Decision trees are versatile algorithms that use statistics to split data based on features, creating a tree-like structure for classification or regression. They are intuitive, interpretable, and handle categorical and numerical data.
Statistics-based measurements, such as Gini impurity or information gain, are often incorporated to guide the splits throughout the tree construction process.
You can learn about decision tree classification in Python in a separate tutorial, or explore decision trees in machine learning using R.
Random Forest
Random Forest is an ensemble learning method that improves prediction accuracy by combining multiple decision trees. It employs sampling to randomly select subsets of features and data for building the trees. The predictions of these individual trees are then aggregated to make the final prediction.
This algorithm is a powerful choice as it introduces diversity and reduces overfitting. The incorporation of diversity allows for a more robust and comprehensive model that captures a wide range of data patterns, and the reduction of overfitting ensures that the model generalizes well to unseen data, making it a reliable and accurate tool for predictive analytics.
We have a separate tutorial on random forest classification, which covers how and when to use the statistics technique in machine learning.
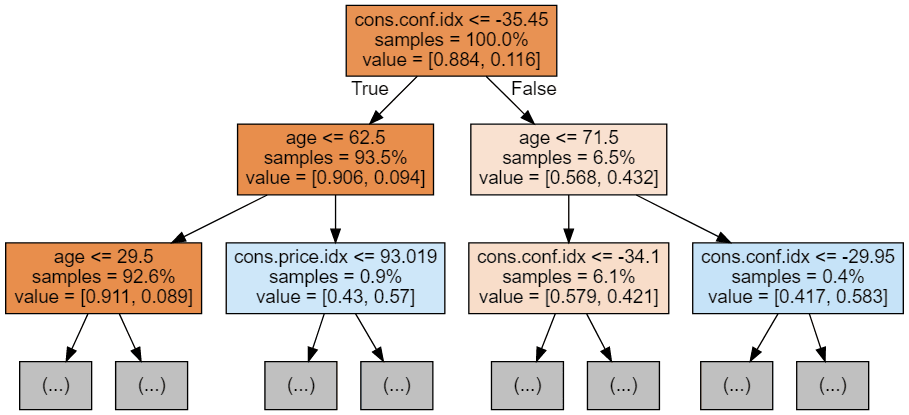
An example of random forest classification
Support Vector Machines (SVM)
SVM is a powerful algorithm that can be used for classification and regression tasks. It uses statistical principles to create a boundary between different groups of data points, making it easier to tell them apart. By optimizing this boundary, SVM reduces the chances of making mistakes and improves overall accuracy.
We have tutorials exploring support vector machines with SciKit learn in Python, as well as SVMs in R.
K-Nearest Neighbors (KNN)
KNN is a simple yet effective algorithm used for classifying data points based on the majority vote of their nearest neighbors. It is suitable for both classification and regression problems and does not require training.
In KNN, statistical measures are utilized to determine the proximity between data points, helping to identify the nearest neighbors. The majority vote of the nearest neighbors is then used to classify or predict the target variable.
Again, you can explore the concept of KKNs in more detail with our K-Nearst Neighbors Classification with scikit-learn tutorial.
Final Thoughts
As we navigate through the exciting era of advancing technology and data-driven decision-making, gaining a solid understanding of statistics becomes invaluable for enhancing our machine learning skills. By delving into the fundamentals of statistics, we unlock the gateway to unleashing the true potential of machine learning.
Whether you're a newbie or a seasoned pro, kickstart your learning journey today with the Statistics Fundamentals with Python and Machine Learning Fundamentals with Python tracks to learn more about the fascinating field of statistical machine learning!
Sources
- All of Statistics (A Concise Course in Statistical Inference) by larry Wasserman
- The Elements of Statistical Learning by Jerome H. Friedman, Robert Tibshirani, and Trevor Hastie
blog
An Introduction to Machine Learning with Julia
blog
Classification in Machine Learning: An Introduction
blog
Supervised Machine Learning
podcast
Data Science and Ecology
tutorial
Seeing Like a Machine: A Beginner's Guide to Image Analysis in Machine Learning
tutorial
